Glenn1Q84

skip-gram

 
  • 2023年 03月04日

词嵌入的目标 获取词在向量空间中的表示，用向量去表示词义→ 获取一个关于词典的矩阵

0. 写在前面

基础知识需要：词嵌入的简单理解（可以我看之前的文章或者视频），统计学的一点点基础概念，神经网络的一丢丢了解

内容预览：

  • skip-gram 的核心思想

  • skip-gram从直觉上的通俗解释

  • skip-gram 损失函数的数学推导

1. 从直觉(intuition)上通俗理解skip-gram

​ 最合乎直觉（intuition）的假设-分布假设：相似的词往往出现在同一语境中（例如，在眼睛或检查等词附近）。

​ ==语义相似的词往往会相邻出现，不相似的词不会相邻出现==

​ 案例：

​ ==颜色标记相同的词（相邻的）语义上是相似的==

​ 目标: 获取词向量的最佳表示，就是获取一个 $\theta \in R^{V×N}$ ，如下，V代表词典大小，N代表每个词对应词向量的维度

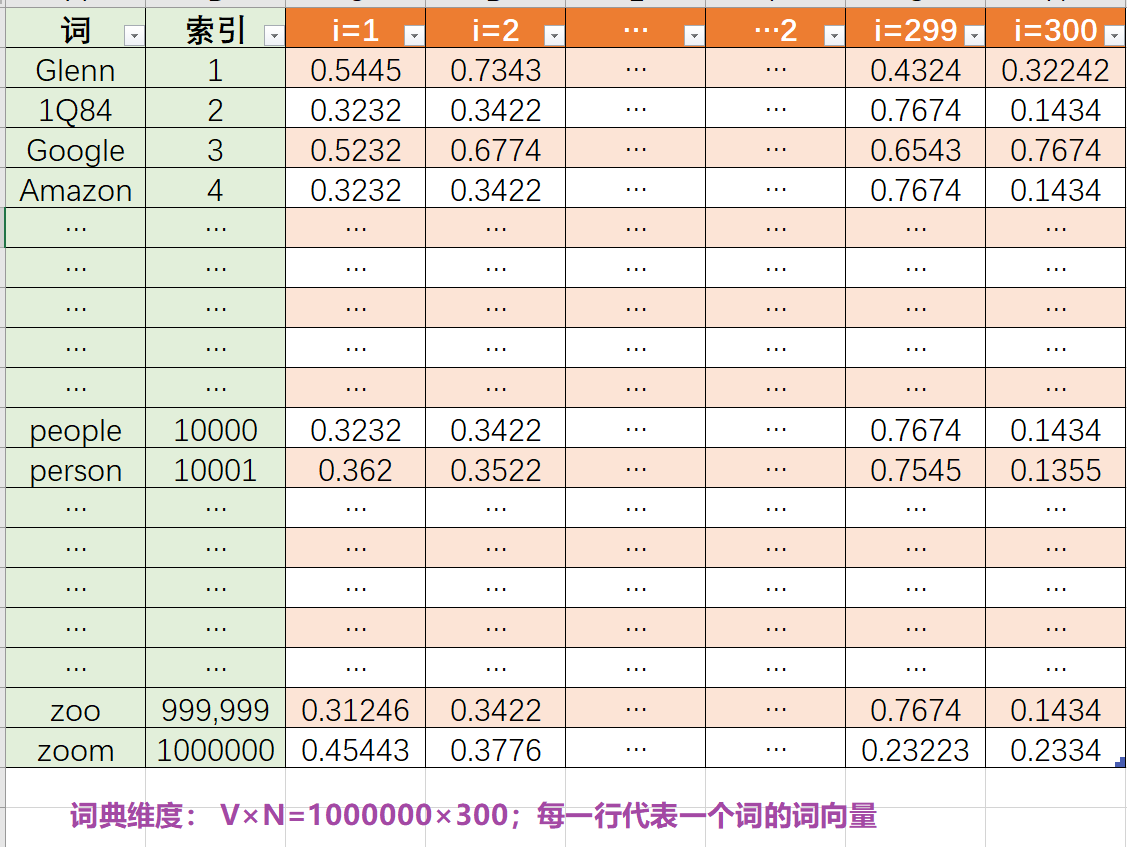
**question 1:  如何 数学化 分布假设（简化：相邻的词语义相似） 实现词向量获取的目标？**

​ maybe 预测（说一句话的时候是一个词一个词蹦出来的，是不是 已知某个词 预测下一个词呢？或者已知某个词 预测周围的语境词呢？）

给定一句话： the man who passes the sentence should swing the sword

pS: ${w_{cj}}$代表第j个相邻词context word，${w_{nci}}$代表第i个非相邻词 not context word

1 2 3 4 5 6 7 8 9 10
the man who passes the ==sentence== should swing the sword
$w_{nc1}$ $w_{nc2}$ $w_{nc3}$ $\pmb }$ $\pmb }$ ==$\pmb {w_{center}}$== $\pmb {w_{c3}}$ $\pmb {w_{c4}}$ $ w_{nc4}$ $w_{nc5}$

目标数学化：通过最大化 给定中心词下相邻词的概率，间接获取词向量表示

\[\underset{\theta}{\operatorname{argmax}}p(w_{c1},w_{c2},w_{c3},w_{c4}|w_{center},\theta)\]

2. 将目标表示成一个神经网络优化任务进行实现：损失函数的推导

\[\underset{\theta}{\operatorname{argmax}}p(w_{c1},w_{c2},...,w_{cC}|w_{center},\theta) \\ C-context\ word 的总数，如(1)中w_{c4}的4\]

step1 简单化任务：假设语境词context word只有一个,实际当中有多个

\[w_{c1},w_{c2},...,w_{cC}→w_{context}\] \[\underset{\theta}{\operatorname{argmax}}p(w_{c1},w_{c2},...,w_{cC}|w_{center},\theta) →\underset{\theta}{\operatorname{argmax}}p(w_{context}|w_{center},\theta)\]

任务定义：

​ task: 基于中心词$w_{center}$预测周围词$w_{context}$

​ input: 中心词 center word $w_{center}$

​ output:语境词or相邻词 context words $w_{context}$

​ optimizing:

\[\underset{\theta}{\operatorname{argmax}}p(w_{context}|w_{center};\theta)\] \[\underset{\theta}{\operatorname{argmax}} p(w_{context}|w_{center};\theta)=\frac{p(w_{context}w_{center})}{p(w_{center})}\]

**question 2 : 如何计算$\frac{p(w_{context}w_{center})}{p(w_{center})}$?**

根据概率公式：

\[P(A_{j}|B)=\dfrac{P(A_jB)}{P(B)}=\dfrac{P(A_j B)}{\sum\limits_{i=1}^n{P(A_i B)}}\]

推导出：

\[\frac{(w_{context}w_{center})} {p(w_{center})}=\frac{p(w_{context}w_{center})} {\sum^V_{i=1}p(w_iw_{center})} \\ V-词典大小，即词典中词的个数 \\ 词典=w_1,w_2,...,w_{context},...,w_V\]

**question 3: 如何计算$p(w_{i}w_{j})$?**

==$w_i,w_j$共同出现的可能性$\Leftrightarrow w_i,w_j$相似程度$\Leftrightarrow w_i,w_j$内积大小，内积越大越相似==

由（9）→（10）

\[p(w_{i}w_{j})\Leftrightarrow similarity(w_i,w_j)\Leftrightarrow w_i^T\cdot w_j\Leftrightarrow exp(w_i^T\cdot w_j) \\w_i,w_j\in R^n\] \[\underset{\theta}{\operatorname{argmax}} p(w_{context}|w_{center};\theta)=\frac{p(w_{context}w_{center})}{p(w_{center})} =\frac{p(w_{context}w_{center})}{\sum^V_{i=1}p(w_iw_{center})}=\frac{exp(w_{context}^T\cdot w_{center})}{\sum^V_{i=1}exp(w_i^T \cdot w_{center})}\]

step2 规范化任务：还原多个context word的目标

由（10）（12）→（13） \(w_{context}→w_{c1},w_{c2},...,w_{cj},...,w_{cC}\)

\[p(x_1,x_2, ..., x_C)=p(x_1)×p(x_2)×,...,×p(x_C)\] \[\underset{\theta}{\operatorname{argmax}}p(w_{c1},w_{c2},...,w_{cC}|w_{center},\theta)=\prod\limits_{j=1}^C\frac{exp(w_{cj}^T\cdot w_{center})}{\sum^V_{i=1}exp(w_i^T \cdot w_{center})}\]

step3 将目标转化为 最小化代价函数cost function $J(\theta)$

对于（13）进行：

  1. 最大化→最小化 加负号
  2. 方便计算： 取对数$log$

得到（14）→（15）

\[\underset{\theta}{\operatorname{argmax}}p(w_{c1},w_{c2},...,w_{cC}|w_{center},\theta)\Leftrightarrow \underset{\theta}{\operatorname{argmin}}p(w_{c1},w_{c2},...,w_{cC}|w_{center},\theta)=-log\prod\limits_{j=1}^C\frac{exp(w_{cj}^T\cdot w_{center})}{\sum^V_{i=1}exp(w_i^T \cdot w_{center})}\] \[J(\theta)= -log\prod\limits_{j=1}^C\frac{exp(w_{cj}^T\cdot w_{center})}{\sum^V_{i=1}exp(w_i^T \cdot w_{center})} = - \sum\limits_{j=1}^{C} log \frac{exp(w_{cj}^T\cdot w_{center})}{\sum^V_{i=1}exp(w_i^T \cdot w_{center})} \\ = -log \sum\limits_{j=1}^{C}exp(w_{cj}^T\cdot w_{center}) + C\cdot {\sum^V_{i=1}exp(w_i^T \cdot w_{center})}\]

计算成本是非常高的，因为每一个中心词都要计算 $C\cdot {\sum^V_{i=1}exp(w_i^T \cdot w_{center})}$,

通过负采样： softmax(从所有词中找出周围词)→sigmoid（分类是否是周围词）

负采样的词如何选择：对词频做归一化，然后做平滑 ，使得出现词频少的部分也能较多的采样

补充说明：

1. 向量的相似性计算

​ 如果一个词的嵌入向量与目标嵌入相似，它就有可能出现在目标附近。为了计算这些密集嵌入之间的相似性，我们依靠这样的直觉：两个向量如果有很高的点积就会相似（毕竟余弦只是一个归一化的点积）：

\(similarity(w,c)\approx w^T\cdot c\\ w,c\in R^n\) 参考文献

  1. Speech and Language Processing (stanford.edu)

  2. [Demystifying Neural Network in Skip-Gram Language Modeling Pythonic Excursions (aegis4048.github.io)](https://aegis4048.github.io/demystifying_neural_network_in_skip_gram_language_modeling)
  3. [Understanding Multi-Dimensionality in Vector Space Modeling Pythonic Excursions (aegis4048.github.io)](https://aegis4048.github.io/understanding_multi-dimensionality_in_vector_space_modeling)
搜索