知识需要：词嵌入

看完篇文章能获得什么：

​ 对词嵌入的深入理解，共现矩阵、Word2vec(skip-gram or CBOW)

​ 训练下游NLP任务时，选择合适的词向量维度

​ maybe 词嵌入方法创新的一丢丢启发

这是原文链接：

https://aegis4048.github.io/understanding_multi-dimensionality_in_vector_space_modeling

词向量维度是多少比较合适呢？

1. 为什么要多维向量空间？

向量空间建模≈词嵌入

Such technique, representing words in a numerical vector space, is called Vector Space Modeling. It is often synonymous to word embedding

A typical vector space model that haven’t went through dimensional reduction has a dimension of V×N where V is a size of unique vocabulary, and N varies based on the choice of modeling method

假设对于Achieve，success合理的向量表示维度为10维

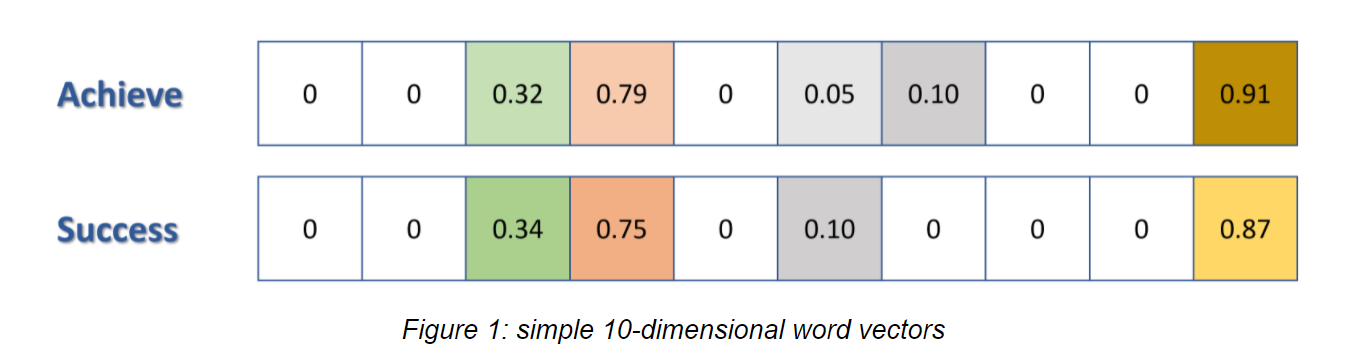
Observe that the vectors in the illustration above looks similar to each other: positions of non-zero values, and values of each cell. Similar word vectors will put similar words close to each other in a vector space, and as a result, “Success” and “Achieve” will have small Euclidean or Cosine Distance.

降维：高维不符合人类的直觉理解（不好想象）、利用率不高，想变成2-3维

One might experience difficulty in trying to visualize the Euclidean or Cosine distance of the word vectors in a 10D vector space. In fact, you can’t visualize anything bigger then 3D. If one attempts to visualize the word vectors in a 2D or 3D space, he will have to represent the word vectors in 2D or 3D space first using dimensional reduction. Let’s assume that such dimensional reduction was performed and the word vectors for “Success” and “Achieve” are reduced to 3D vectors. The word vectors will then look like this:

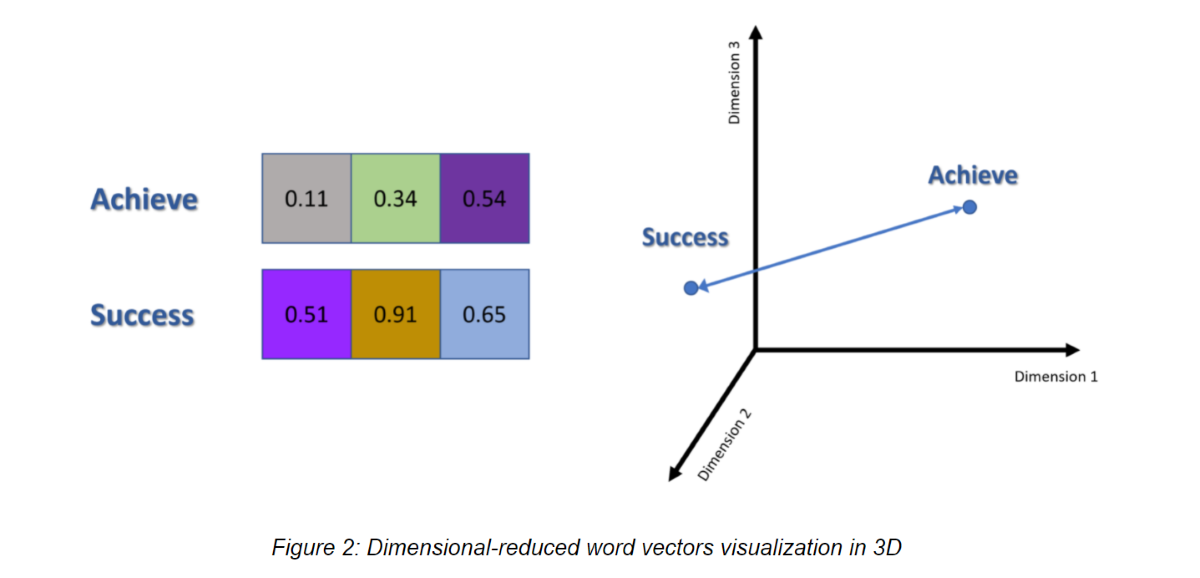
==Observe the dissimilarity== between two word vectors and their positions within the 3D vector space. This is because 3 dimensions are not enough to capture all relationship among words and as a result fails to maintain the semantic relationship between two similar words, “Success” and “Achieve”.

==划重点：低维向量难以表示复杂语义信息==，

维度越高越好吗？

​ 个人的猜测：从符合直觉的角度来思考：维度的大小与词的复杂度（语料=语境）成正比。

​ 在语料给定（意味着语境给定）的情况下 能完美表示词义的词的维度是确定的

例子：

​ 不同语料：zhihu VS 维基百科 自然语言处理

2. 向量空间建模技术

2.1 Co-Occurence Matrix

2.1.1 What is Co-Occurence Matrix?

The value of N for co-occurence matrix is the size of unique vocabulary. In the other words, co-occurence matrix is a square matrix of size $V×V$.

Consider a co-occurence matrix with a fixed window size of $n=1$. Setting window size $n=1$ will tell the model to search adjacent context words that are positioned directly left or right of a center word. The matrix is contructed using the following two input documents:

Document 1: “all that glitters is not gold”

Document 2: “all is well that ends well”

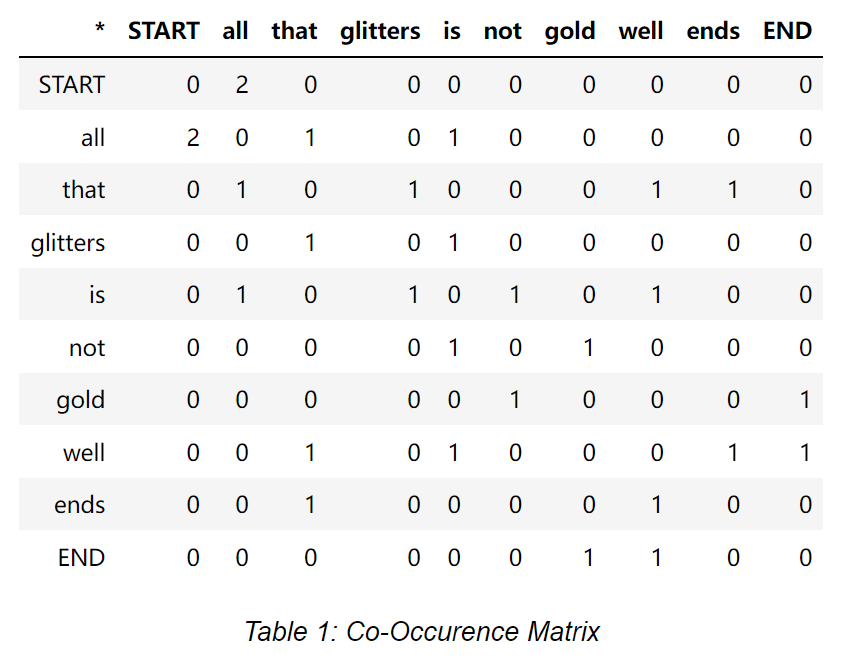
Notes: START and END tokens

In NLP, we often add START and END tokens to represent the beginning and end of sentences, paragraphs or documents. In thise case we imagine START and END tokens encapsulating each document, e.g., “START All that glitters is not gold END”, and include these tokens in our co-occurrence counts.

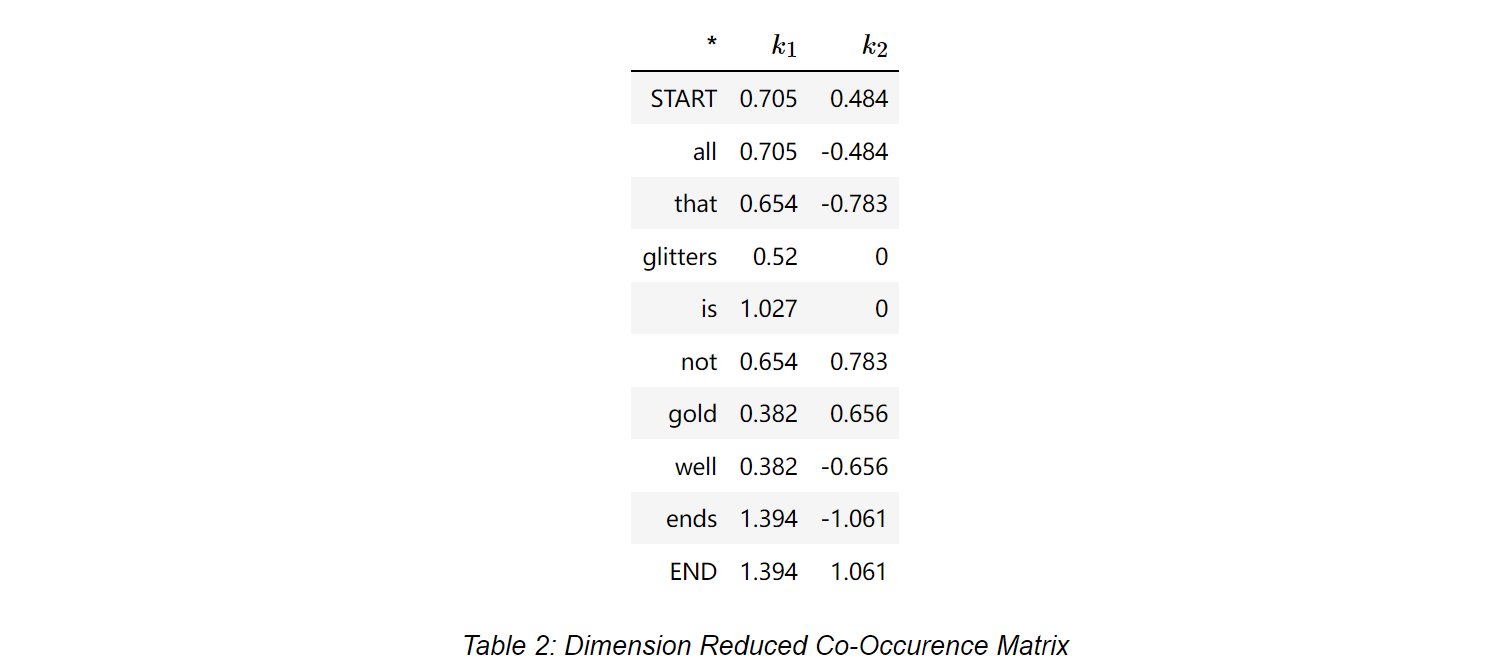
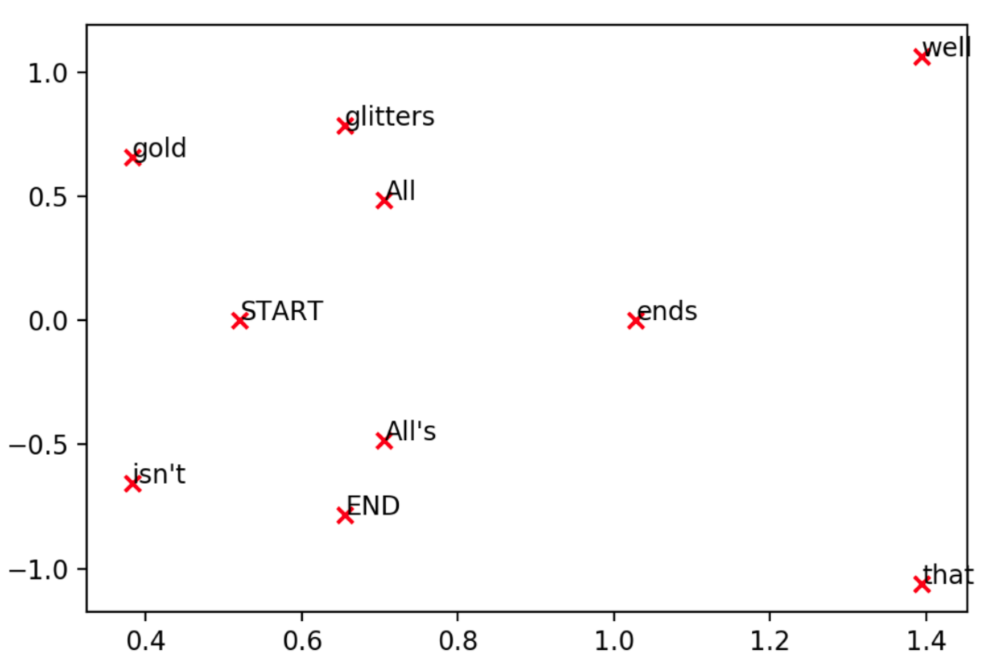
2.1.2 dimensional reduction

This co-occurence matrix is essentially a vector space model of $V×V$-dimensional matrix, in which $V=10$ However, in most NLP tasks, this co-occurence matrix goes through PCA or SVD for dimensional reduction and decomposed into a new $V×K$($K=2$)-dimensional matrix.

2.2 Word2Vec

2.2.1 Intuition

Contrary to frequency-based methods, prediction-based methods are more difficult to understand. As the name ‘prediction’ implies, their methodologies are based on predicting context words given a center word (Word2Vec: Skip-Gram):

\(P(w_{context}∣w_{center})\) or predicting a center word given context words (Word2Vec: Continuous Bag of Words)

\[P(w_{center}∣w_{context})\]

Prediction-based methods use neural network algorithm, which means that we have to worry about the number of neurons (weights) in a network. In Word2Vec model, the model matrix has a dimension of $V×N$, where $V$ is the size of unique vocabulary and the size of $N$ is the number of neurons in a network.

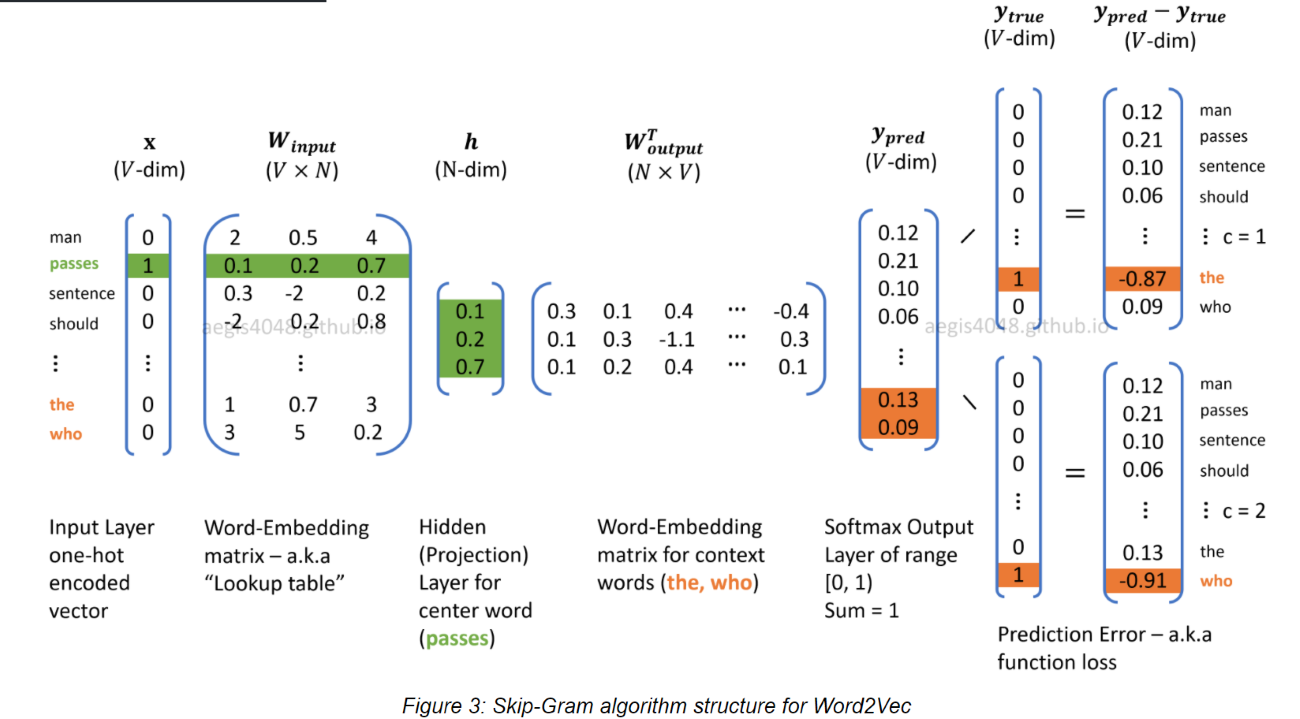
2.2.2 How to choose the best $N$?

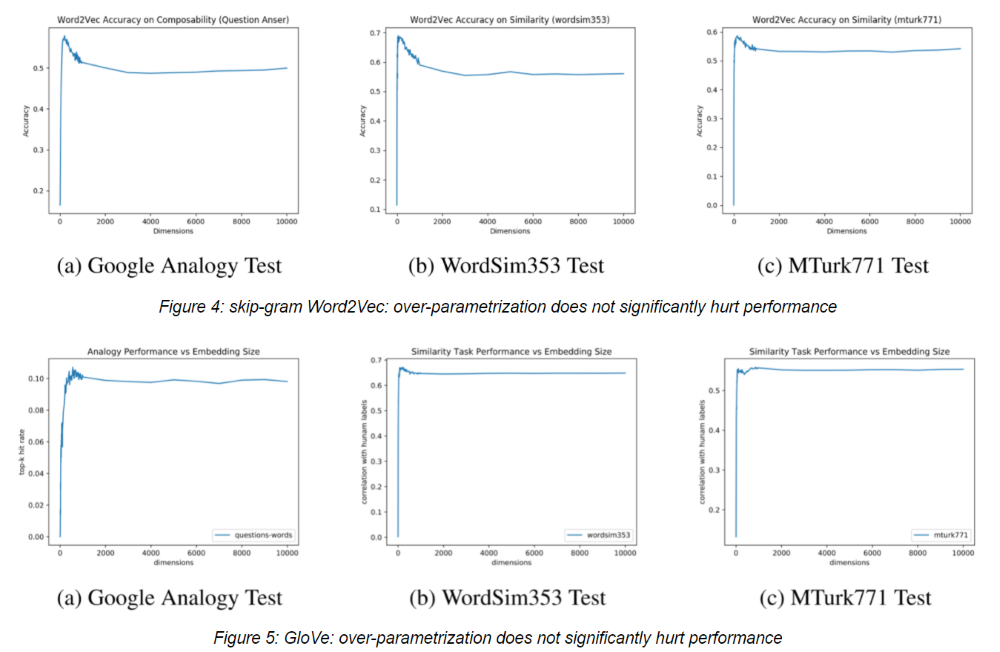
3. 为什么合适的词向量维度是重要的？

First, high dimensionality leads to high computational cost especially for Co-Occurence.

Second, dimension is a critical parameter in word embedding. Too low dimension leads to underfitting and makes your model not expressive enough to capture all possible word relations.