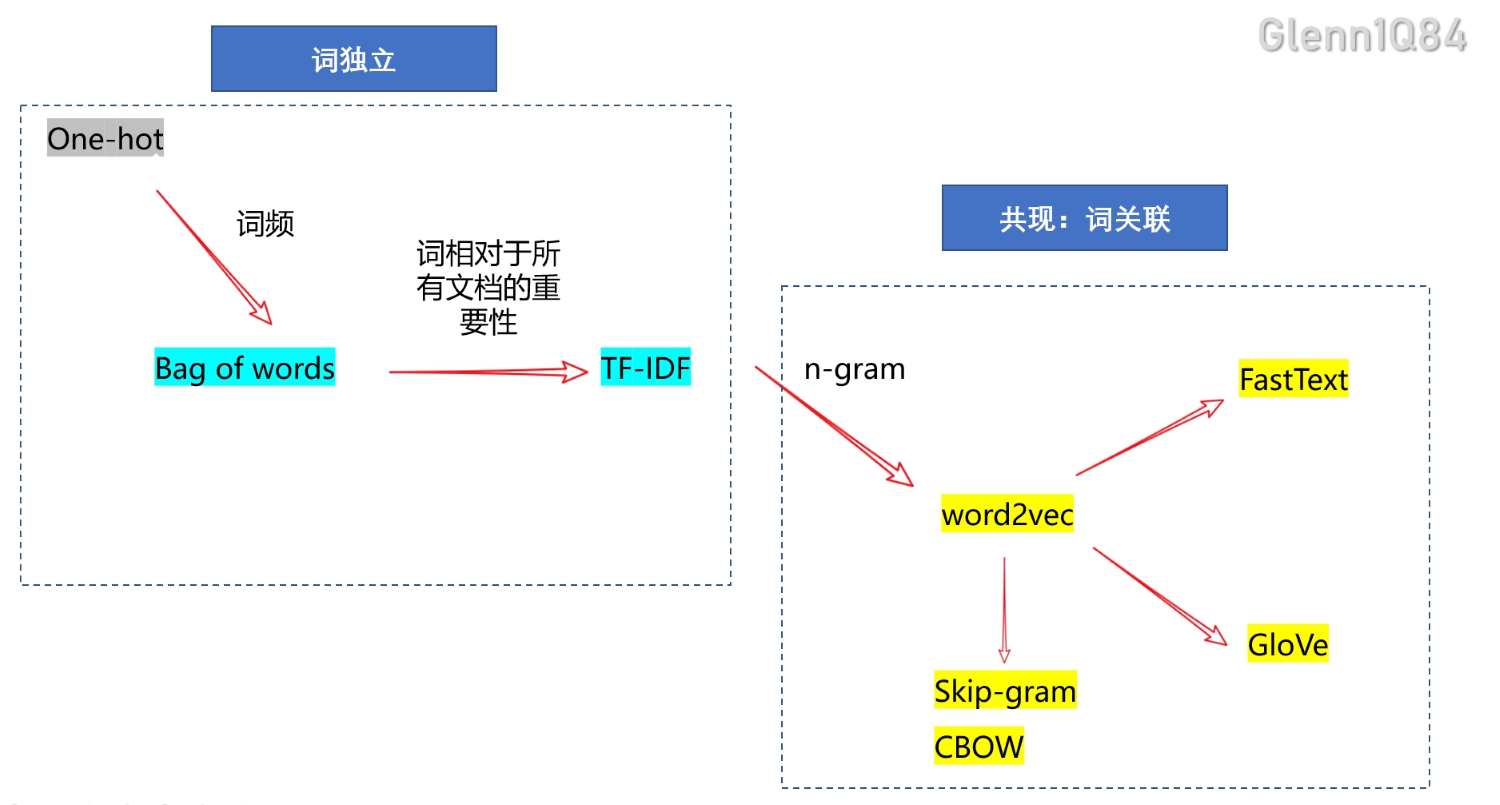
why? From LSA(latent semantic analysis) and skip-gram to GloVe
- LSA: 基于全局词频的稀疏矩阵, 在词义推理任务上表现较差、
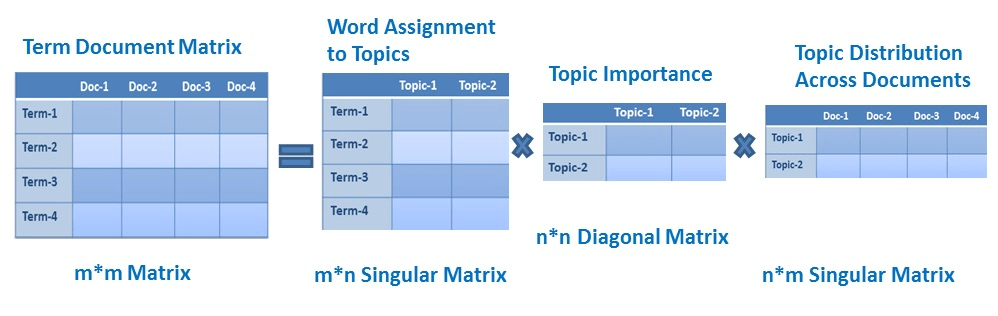
- skip-gram: 局部共现,没能利用全局统计信息

- GloVe: 全局统计信息+共现=全局共现词频
GloVe: Global Vectors for Word Representation
理论基础:
- ①在指定窗口大小内共同出现的词$w_i,w_j$具有相似的语义
- ②$w_i,w_j$共现的次数越多,语义越相似
- ③$w_i,w_j$之间的距离$d$越远,语义越不相似
已有信息:
- 语料,及其共现矩阵$X$, 其中$X_{ij}$表示语料中$w_i,w_j$在指定窗口大小能共同出现的次数
- 向量点积$\vec{w}_i^T \vec{w}_j$表示$w_i,w_j$之间的相似性,越大越相似
构造训练目标:最小化损失函数
根据理论①②:
\[w_i,w_j的相似性 = w_i,w_j的共现次数\] \[\begin{equation}\vec{w}_i^T \vec{w}_j = \log X_{ij}.\end{equation}\]加上一个偏置
\[\begin{equation}\vec{w}_i^T \vec{w}_j + b_i + b_j = \log X_{ij}\end{equation}\] \[\begin{equation}Loss = \vec{w}_i^T \vec{w}_j + b_i + b_j-\log X_{ij}\end{equation}\]对所有词计算损失,V代表词典大小
\[\begin{equation}J = \sum_{i=1}^V \sum_{j=1}^V \; \left( \vec{w}_i^T \vec{w}_j + b_i + b_j - \log X_{ij} \right)^2 \end{equation}\]这样会存在一个问题,这样对所有的共现都是平等的,即便有些词很少或者基本不共现。很少共现的词仅能提供更少的信息且具有较大的噪音,$X_{ij}=0$的单元占据了X的较大部分(75-95%)。因此我们希望关注共现更多的词。
So 对损失加上一个权重函数$f(X_{ij})$
\[\begin{equation}J = \sum_{i=1}^V \sum_{j=1}^V \; f\left(X_{ij}\right) \left( \vec{w}_i^T \vec{w}_j + b_i + b_j - \log X_{ij} \right)^2 \end{equation}\]-
共现次数越大的赋予较高权重,较小的赋予较低权重。所以这个权重函数要是非递减函数(non-decreasing);
-
但我们也不希望这个权重过大(overweighted),当到达一定程度之后应该不再增加;
-
如果两个单词没有在一起出现,也就是$X_{ij}=0$,那么他们应该不参与到$loss function$的计算当中去,也就是$f(x)$要满足$f(0)=0$
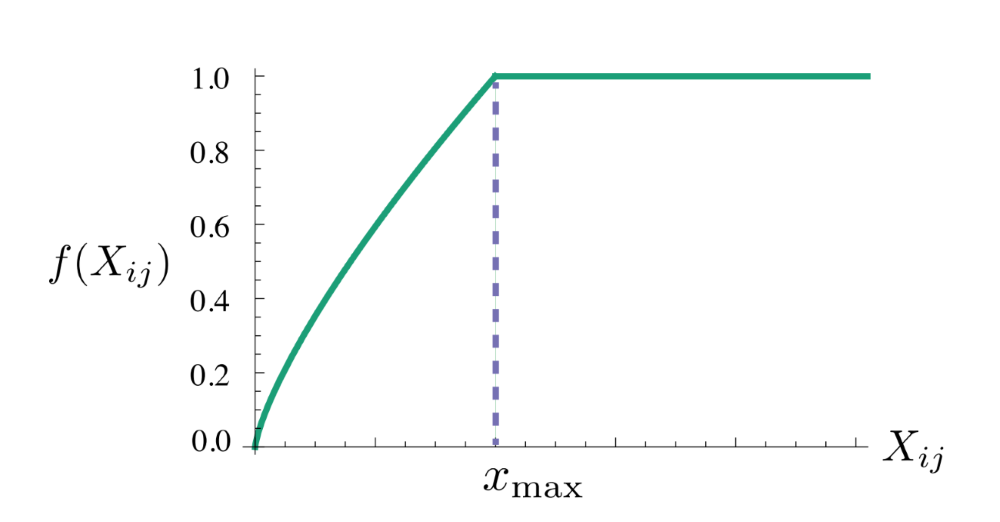
PS: 对$X_{ij}$较高的$w_i,w_j$ 加一个权重,个人理解类似于 一种限制,让最小化Loss时更关注相似词
想象一下,最小化Loss1,原本对所有共现词是无差别的;
现在加了个$f(X_{ij})$:
- 当$w_{i},w_{j}$共现次数较多时$X_{ij}$较大
最小化$Loss2$,$f(X_{ij})$较大→需要$Loss(w_i,w_j;X_{ij})$变得更小 也就是更关注共现次数较大的$w_{i},w_{j}$了
- 当$w_{i},w_{j}$共现次数较少时$X_{ij}$较小
最小化$Loss2$,$f(X_{ij})$较小→$Loss(w_i,w_j;X_{ij})$不太需要变得更小 也就是不怎么关注共现次数较少的$w_{i},w_{j}$了
\[Loss1=Loss(w_i,w_j;X_{ij})\]\(Loss2=f(X_{ij})*Loss(w_i,w_j;X_{ij})\) ③$w_i,w_j$之间的距离$d$越远,语义越不相似
第一时间是不是会想到直接乘以一个权重的方式:
\(X_{ij}=\frac{1}{d+1}X_{ij}; \quad d\in(0,window\ size)\) 个人猜测,这可能会对$X_{ij}$本身的信息造成影响(对$X_{ij}$进行缩放),而这个时候想要把距离信息直接加入到共现词频信息$X_{ij}$中,且不对$X_{ij}$本身造成影响
所以去扒拉了一下原文的代码实现,发现真正计算时是这样的
\[X_{ij}=X_{ij}+\frac{1}{d+1}; \quad d\in(0,window\ size)\]完美!!!!!
论文原文
GloVe: Global Vectors for Word Representation - ACL Anthology
参考文献
论文代码实现
